Clojure deftype with `unsynchronized-mutable`
In this post let’s take a closer look at why the ^:unsynchronized-mutable is used in this Clojure code snippet and learn some Java in the process.
(ns user
(:import (net.thisptr.jackson.jq JsonQuery Scope Output)
(com.fasterxml.jackson.databind JsonNode)))
(definterface IGetter
(^com.fasterxml.jackson.databind.JsonNode getValue []))
(deftype OutputContainer [^:unsynchronized-mutable ^JsonNode container]
Output
(emit [_ output-json-node] (set! container output-json-node))
IGetter
(getValue [_] container))
(defn query-json-node [^JsonNode data ^JsonQuery query]
(let [output-container (OutputContainer. nil)]
(.apply query (Scope/newEmptyScope) data output-container)
(.getValue output-container)))
Note that this code snippet is a bit trimmed down for clarity. The full code can be found here.
Introduction
I was working on clj-jq:
a Clojure library whose goal is to make it easy to embed a jq processor directly into an application and that this application can be compiled with the GraalVM native-image.
clj-jq was intended to be a thin wrapper for the jackson-jq Java library.
The exact use cases of the clj-jq are left out for future blog posts.
Wrapper
The jackson-jq provides a nice example class that helped me to start implementing the wrapper.
I’ve taken a straightforward approach to create a Clojure library: just “translate” the necessary Java code to Clojure using the Java interop more or less verbatim, parameterize the hardcoded parts, refactor here and there, and the result would be a new library.
The “translation” went as expected until I had to deal with a code that implements the Output interface:
final List<JsonNode> out = new ArrayList<>();
q.apply(childScope, in, out::add);
In the example an instance of ArrayList and some Java magic was used (we’ll talk about what and why in the appendix).
Since Clojure functions doesn’t implement Output interface I can’t pass a function, therefore I’ve “translated” the code using reify approach as shown below:
(defn query-json-node [^JsonNode data ^JsonQuery query]
(let [array-list (ArrayList.)]
(.apply query (Scope/newChildScope root-scope) data
(reify Output
(emit [this json-node] (.add array-list json-node))))
(.writeValueAsString mapper ^JsonNode (.get array-list 0))))
it worked, but I wasn’t happy about it.
Using an ArrayList in such a function might be OK for an example.
But for a library something more specialized is desired because of several reasons:
- the
ArrayListwill always hold just one value; - allocating an
ArrayListandreifying is not super cheap;
It got me thinking about how to make something better.
Requirements
The requirements for the Output implementation:
- a specialized and efficient class;
- that class has to act as a mutable1 container that holds one value;
Efficiency is desired because the library is intended to be used in “hot spots” of an application.
Before starting to work on clj-jq I expected that the work would not require writing any Java code because that would complicate the release of the library.
Therefore, I aimed to implement my Output class in Clojure.
Also, gen-class feels a bit “too much” for this little problem.
Implementation
The Output interface defines behaviour, therefore I’ve chosen the deftype.
The implementation class needs mutable state to hold one value.
deftype has two options for mutability of fields: volatile-mutable and unsynchronized-mutable.
The deftype docstring advices that the usage of both options is discouraged and are for “experts only”.
I skipped the first part of the advice because I wanted to learn a good lesson.
For the second part my thinking was that if I used the options “correctly” I could consider myself an “expert” :-)

What are the implications of those two deftype field options:
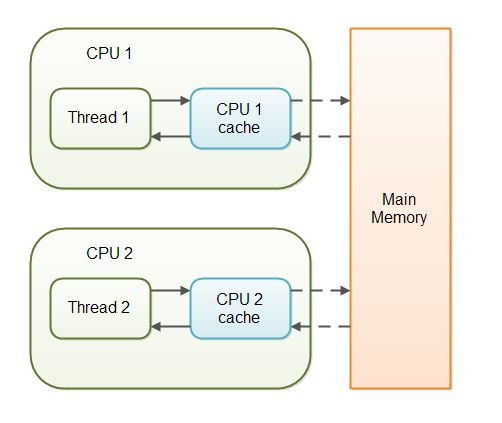
volatile-mutablemeans that field is going to be marked asvolatile. Volatile in Java means that the variable is stored in the main memory and not in the CPU cache. This provides a data consistency guarantee that all threads will observe the updated value immediately2. Therefore, thevolatile-mutableoption is OK to be used when the field is going to be written to by one thread and read from multiple threads.- The field marked with
unsynchronized-mutableoption is backed by a regular Java mutable field. In contrast tovolatile-mutable, theunsynchronized-mutablevalue might be stored in the CPU cache. Therefore,unsynchronized-mutablefield is OK when used in single-threaded3 contexts.
Since the scope in which my container class is going to be used is small and short-lived (can be considered as an internal implementation detail) and not multi-threaded,
I can choose an option that promises a better performance: unsynchronized-mutable4.
Go back to the code
The most interesting bit of the entire snippet is the deftype:
(deftype OutputContainer [^:unsynchronized-mutable ^JsonNode container]
Output
(emit [_ output-json-node] (set! container output-json-node))
IGetter
(getValue [_] container))
The class generated by deftype will be named OutputContainer.
It has one mutable field: container that is hinted to be of JsonNode type.
By declaring a method mutable deftype generates the set! assignment special form to allow mutation of the field.
Usage example of the OutputContainer:
(defn query-json-node [^JsonNode data ^JsonQuery query]
(let [output-container (OutputContainer. nil)]
(.apply query (Scope/newEmptyScope) data output-container)
(.getValue output-container)))
In the function query-json-node we create an instance of the OutputContainer.
Then pass it to apply method of the JsonQuery.
Somewhere in the apply the Output::emit will be called5.
Finally, we take out the value of JsonNode type from the output-container instance.
Summary
unsynchronized-mutable is relatively rarely used in the wild: only 776 out of 13,362 uses of deftype according to GitHub code search as of 2021-09-09.
But when we do understand the implications, and we need exactly what the option provides, we can go ahead and use it despite what the docstring says.
And don’t forget to test your code!
Appendix
Once again, let’s look at this piece of code:
final List<JsonNode> out = new ArrayList<>();
q.apply(childScope, in, out::add);
Here method reference to add of a List<JsonNode> object is used as an argument to a method that expects Output type.
How does it work?
A bit of Java theory
Any interface in Java with a SAM (Single Abstract Method) is a functional interface. And for an argument of a functional interface type one can provide either:
- a class object that implements the interface,
- lambda expression.
A method reference can replace a lambda expression when passed and returned value types match. You can use whichever is easier to read.
Why does it work anyway?
The Output is an interface that provides just one method emit (default methods doesn’t count).
Therefore, it is a functional interface (however, not annotated as such).
We can provide a lambda expression where a functional interface type is expected. Also, in the same place we can provide a method reference whose types match the expected input-output types.
What are the expected types for Output::emit?
JsonNode for input and void for output.
When a variable is of type List<JsonNode> then the add method accepts JsonNode type and returns void.
We can see that types match, therefore method reference to out::add can be used when Output is required. Voila!
Footnotes
Mutable and not-shared might be OK. ↩︎
Note that writes are not atomic for the volatile value. ↩︎
Consult the Java Memory Model docs to learn more. ↩︎
A proper discussion on
deftypemutability and here ↩︎